Пределы
По своей сути предел - это то, чему равна функция в тот момент, когда аргумент почти равен (но не равен) какому-то значению.Рассмотрим следующий график. Перед Вами график функции y=1/x.
Мы видим, что в той точке, где x=0, функция не существует. Да и помним это, подставив в выражении x=0: y=1/0, а деление на 0 невозможно, что мы прекрасно помним со школы. Однако, чему будет равна функция, если на место х мы подставим не 0, а какое-либо число максимально близкое к 0? Подставим сначала значение x=0.1: y=1/0.1=10. Теперь возьмем x=0.001: y=1000. А что, если взять x=0.00000001? y снова увеличиться во столько же раз, во сколько уменьшился x. Следовательно, если мы примем, что x стремится к 0, то есть x максимально близок к нулю, y будет равен бесконечности (∞).
А что если х будет приближаться к 0 с другой стороны? То есть сначала возьмем значение не 0,1, а -0,1, затем -0,0001 и т.д. Как мы видим из графика, чем меньше отрицательное число, тем меньше значение аргумента. То есть, если х максимально близок к 0, но со стороны отрицательных чисел, y будет равен минус бесконечности (-∞).
Теперь рассмотрим следующий момент в этом же графике. Чем больше значение x, тем меньше значение y. Значит когда x стремится к бесконечности ∞, y стремится к 0.
То же самое мы видим по другую сторону графика, если х стремится к -∞, у также стремится к нулю.
Запись предела
Посмотрим на 2 следующие записи:Первая из них звучит примерно так: "Предел функции 1/x, при х стремящемся к минус 0, равен минус бесконечности". И означает то же самое, что мы рассмотрели в параграфе 2.
Вторая запись звучит следующим образом: "Предел функции 1/х, при х стремящемся к 0, равен бесконечности". И означает то же самое, что мы рассмотрели в параграфе 1.
Как записывать предел:
- В начале стоит слово lim, которое обозначает "предел" (от англ. limit).
- Снизу подписывается к какому значению стремится переменная.
- Затем пишится сама функция, которая содержит эту переменную.
- После знака равно пишется значение предела, то есть пишется то, к чему стремится вся функция, если переменная стремится к какому-то значению.
Моменты, которые нужно запомнить:
- Под словом "стремится" подразумевается "почти равно".
- Само обозначение lim пишется каждый раз, до тех пор, пока в функции есть переменная, которая стремится к какому-либо значению.
- Если переменная стремится к какому-то значению с правой стороны графика (то есть немного больше, чем это значение), оно записывается с плюсом после числа.
- Если переменная стремится к какому-то значению с левой стороны графика (то есть немного меньше, чем это значение), оно записывается с минусом после числа.
- Если после значения, к которому стремится переменная не стоит ни +, ни -, значит либо это не имеет значения, либо подразумевается, что переменная немного больше данного значения.
Решение примеров с пределами
Алгоритм решения простейших пределов примерно такой:- Подставляем в функцию то значение переменной, к которому эта переменная стремится.
- Решаем, как обычный пример, помня о следующих правилах:
- Любое число (кроме 0 и ∞) делить на ноль = ∞
- Любое число (кроме 0 и ∞) делить на ∞ = 0
- ∞ плюс/умножить на ∞ = ∞
- 0 плюс/минус/умножить на 0 = 0
- И прочие случаи. Размышляйте логически. И посмотрите раздел "неопределенности пределов".
Попробуем разобрать следующие 5 примеров:

Как это решалось? Арк-тангенс(arctg или tan-1) - это ограниченная функция. То есть значения функции лежат в пределах от 0 до 2π. 3x при x, стремящемся к бесконечности, равно бесконечности, так как 3 умножить на бесконечность будет ни что иное, чем бесконечность. А ограниченная функция плюс бесконечность дают бесконечность.
Пример 2:
Как это решалось? Обе функции: корень из х и 6 в степени х при х, стремящемся к бесконечности, равны бесконечности. А ∞ умножить на ∞ равно ∞.
Пример 3:
Как это решалось? Обе функции: 2 в степени х и 9 в степени х при х, стремящемся к бесконечности, равны бесконечности. А ∞ + ∞ равно ∞.
Пример 4:
Как это решалось? cos(x) при x→0 равен 1. А x3 равен 0. Так как 0 в любой степени будет 0. А 0 разделить на 1 даст 0.
Пример 5:
Как это решалось? Подставив под x три, мы получаем в знаменателе ноль. А любое число, деленное на ноль, даст бесконечность.
Неопределенности пределов
Однако, не все пределы решаются так легко, просто подставив значение переменной в функцию. Иногда после подстановки переменной мы можем получить следующие выражения, которые заставляют нас немного помучиться.
Пример 1.1:
Пример 2.1:
Пример 2.2:
Пример 3.1:
Пример 3.2:
Пример 4.1:
Пример 5.1:
Пример 5.2:
Эквивалентные преобразования
Эквивалентные преобразования могут значительно упростить нам жизнь, если их правильно использовать. Они позволяют нам заменить одно выражение на другое, более удобное, если x→0. Вот все эти случаи:
sin x ∼ x
cos x ∼ 1-x2/2
tg x ∼ x
arcsin x ∼ x
arctg x ∼ x
(1 + x)a ∼ 1 + ax
ln(1+x) ∼ x
ex ∼ 1 + x
sh x ∼ x
ch x ∼ 1 + x2/2
th x ∼ x
Рассмотрим всего один пример и сразу станет все понятно:
Пример:
Если после подстановки значения переменной в предел мы получаем неопределенность вида 0/0 или ∞/∞, то решить данный предел можно, найдя производные делителя и знаменателя:
мы получаем неопределенность вида 0/0 или ∞/∞, то решить данный предел можно, найдя производные делителя и знаменателя:  .
.
Автор статьи: Александр Картышев
Правило Лопиталя
При помощи формулы Лопиталя можно найти значение предела при неопределенности вида 0/0 или ∞/∞. Однако, для её использования, нужно уметь решать производные. Итак, правило Лопиталя:
 мы получаем неопределенность вида 0/0 или ∞/∞, то решить данный предел можно, найдя производные делителя и знаменателя:
мы получаем неопределенность вида 0/0 или ∞/∞, то решить данный предел можно, найдя производные делителя и знаменателя:  .
.
Рассмотрим пример:
Автор статьи: Александр Картышев


















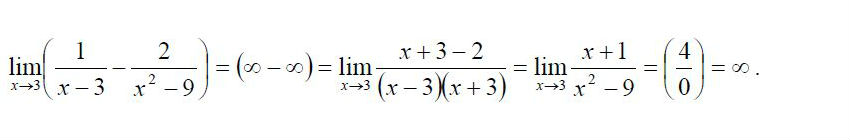






Комментариев нет:
Отправить комментарий